АРХИВ СТАТЕЙ ЖУРНАЛА «МОЙ КОМПЬЮТЕР» ЗА 2003 ГОД

В графском парке

• Все журналы \ Номер 52/275 `2003 от 29.12.2003 \ В графском парке

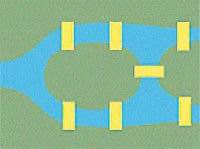
Юрий ДОВГАНЬ freeyuran@ukrpost.net

Продолжение, начало см. в МК № 33-34, 38, 43, 46, 48 (256-257, 261, 266, 269, 271).
В прошлый раз мы остановились на проблеме эйлеровых циклов в графах. С большой долей серьезности не побоюсь назвать ее эйлеровой проблемой. Почему так? Давайте на некоторое время перенесемся в далекий 1736 год.

Именно в этом году великий математик Леонард Эйлер доказал невозможность существования решения задачи о кенигсбергских мостах. Заключается задача в следующем. Город Кенигсберг (более известный нам сейчас как Калининград) исторически поделен на четыре части: правый и левый берега речки Прегель и два острова. Разные части этого города в то время соединялись семью мостами. Требовалось найти маршрут, который бы проходил по каждому мосту ровно один раз и в итоге заканчивался бы в начальной точке пути.

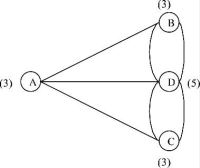
На рисунке отчетливо видны все 4 части города зеленого цвета, речка и 7 мостов желтого цвета. В виде графа город можно представить следующим образом:

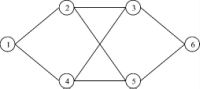
Пусть A, B, C, D — вершины, соответствующие частям Кенигсберга. Ребра графа представляют собою мосты, которые соединяют разные части города. Возле каждой вершины в скобочках указана ее степень — количество мостов, которые соединяют эту часть города с соседними частями. Идея доказательства невозможности такого маршрута состоит в следующем: при посещении каждой вершины мосту, по которому мы вошли в часть города, должен соответствовать мост, по которому мы ее покинем. Другими словами, количество ребер, инцидентных каждой вершине должно быть четным, что и доказал Эйлер в своей теореме, огорчив всех своих предшественников. Вот такая вот грустная история :-).

Теперь машина времени несет нас в 1859 год. Другой математик, на сей раз ирландец, сэр Уильям Гамильтон, придумал игру, в которой требовалось обойти цикл всех ребер додекаэдра (ничего себе игра :-)), посещая каждую вершину единожды. Разумеется, должны быть посещены все вершины. Как оказалось, сэру Гамильтону больше повезло, чем Эйлеру — цикл он таки нашел, хоть и не без усилий. Сейчас и мы с вами, дорогие читатели, поиграем в интересную игру — нахождение гамильтоновых циклов графа :-).

Часть 12. Гамильтоновы циклы и гамильтоновы графы.

Итак, гамильтоновым циклом в графе называется цикл, который содержит каждую вершину этого графа (то есть проходит по всем вершинам по одному разу). Следовательно, граф, содержащий гамильтонов цикл, называется гамильтоновым графом. Таких циклов в графе может быть несколько.

Достаточным условием «гамильтоновости» графа может служить такая теорема: если в графе с N вершинами для любых его двух несмежных вершин v1 и v2 справедливо неравенство St(v1)+St(v2)N, где St(vi) — степень i-й вершины, то в нем существует цикл Гамильтона. Поскольку теорема отображает лишь достаточные условия существования гамильтоновых циклов в графе, то найдутся и такие экземпляры, которые не удовлетворяют неравенству теоремы, но в то же время являются гамильтоновыми. Другими словами, если неравенство справедливо, то граф гарантировано будет содержать гамильтонов цикл. В противном же случае мы не можем утверждать наверняка отсутствие оных.

Пускай на входе имеется связный неориентированный граф G с N вершинами. Требуется найти все гамильтоновы циклы графа G, если таковые в нем имеются.

К большому нашему сожалению, науке пока еще неизвестны эффективные методы решения поставленной задачи. Поэтом предлагается воспользоваться «дешевым и сердитым» методом перебора с возвратом, в народе именуемым как back-tracking алгоритм.

А выглядит он следующим образом. Начиная с определенной вершины (пускай это будет вершина с номером 1) будем продвигаться вперед по графу, включая очередное ребро в гамильтонов цикл. При найденных первых k компонент решения рассматриваем ребра, которые выходят из последней вершины. Если находим ребро, которое ведет в неучтенную ранее вершину, добавляем новую вершину в цикл — она становятся просмотренной. (k+1)-я компонента решения при этом получена. При отсутствии такой вершины возвращаемся к предыдущей и ищем другие смежные с ней. Цикл считается найденным, если просмотрены все вершины графа, и из последней можно достичь начальной. Такой цикл можно вывести на экран и продолжить поиск других.

Давайте попробуем записать все это на инопланетном языке :-).

Вспомним некоторые глобальные типы:

Вот и все! В результате будем иметь на экране все существующие гамильтоновы циклы в заданном графе. Каждый из них начинается в начальной вершине, заканчивается в ней же и содержит все вершины графа.

К примеру, для графа

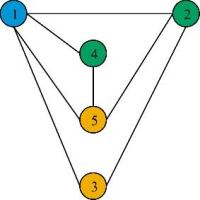
программа выдаст следующие циклы с порядком вершин:

Здесь указан порядок вершин. Разумеется, каждый цикл замыкается в 1-й вершине, то есть начальной.

Часть 13. Раскраски

Прежде чем начинать вчитываться в строки этой главы, всем читателям-испытателям советую взять в руки политическую карту мира. Если внимательно присмотреться, то можно заметить некоторую закономерность раскраски территорий стран: на карте вы не найдете ни одной пары соседних государств, раскрашенных в одинаковый цвет. Ничего особенного, правда? Ведь соседние государства для удобства по-разному окрашены, дабы не сливались их границы.

Как ни странно, такими вещами тоже занимается теория графов. Представим, что политическая карта мира — это граф. Здесь каждое государство представляет собой его вершину, границы — ребра, а материки и острова — компоненты связности графа. Теперь попробуем определиться с понятием раскраски графа. Это произвольная функция f: VC, где V — множество вершин графа, а C={1, 2, 3, …, k} — конечное подмножество натуральных чисел. Более простым языком, функция раскраски f каждой вершине графа ставит в соответствие некоторое натуральное число (раскрашивает вершины цветами из определенной палитры). Если каждый цвет пронумеровать натуральным числом, то такой палитрой как раз и выступает множество С.

Отсюда можно заметить, что вершины графа можно раскрашивать как угодно: хоть все одним цветом. Напрашивается еще одно определение. Правильной раскраской графа называется такая его раскраска, когда любые его две смежные вершины раскрашены в разные цвета. То есть f(u)f(v) для любых двух смежных вершин u и v.

Давайте же попробуем научиться раскрашивать графы правильно :-)! Вместо названий цветов будем использовать натуральные числа. Метод правильного раскрашивания базируется на такой простой идее: раскрашивать очередную вершину в минимально возможный цвет. Для реализации метода мы используем множество цветов:

Получается, что каждой вершине будет приписан цвет в виде числа. Для этого введем переменную

которая покажет, что значение элемента Col[j] определяет номер цвета вершины j. Здесь j принадлежит множеству вершин {1, 2, …, N}, а Col — множеству цветов {1, 2, …, k} правильной раскраски графа. Очевидно, что kN.

Правильная раскраска получена. Давайте рассмотрим примерчик, который поможет нам осознать весь смысл алгоритма:

После запуска процедуры Colorize имеем на выходе массив Col:

Таким образом, мы с вами научились раскрашивать графы правильно. К счастью, это еще не пик совершенства :-).

(Продолжение следует)

Идёт загрузка...

Данную страницу никто не комментировал. Вы можете стать первым.

Ваше имя:
Ваша почта:
Комментарий:
Введите символы или вычислите пример: * Обновить