 
|
|
Новости
Статьи
Магазин
Драйвера
Контакты
RSS канал новостей
Программаторы 25 SPI FLASH
Адаптеры Optibay HDD Caddy
Драйвера nVidia GeForce
Драйвера AMD Radeon HD
Игры на DVD
Сравнение видеокарт
Сравнение процессоров
В конце марта компания ASRock анонсировала фирменную линейку графических ускорителей Phantom Gaming. ... Компания Huawei продолжает заниматься расширением фирменной линейки смартфонов Y Series. Очередное ... Компания Antec в своем очередном пресс-релизе анонсировала поставки фирменной серии блоков питания ... Компания Thermalright отчиталась о готовности нового высокопроизводительного процессорного кулера ... Компания Biostar сообщает в официальном пресс-релизе о готовности флагманской материнской платы ... |
АРХИВ СТАТЕЙ ЖУРНАЛА «МОЙ КОМПЬЮТЕР» ЗА 2003 ГОДДва кита математики
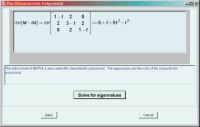
Константин НОСОВ k_n@ua.fm Окончание, начало см. в МК, №48 (271). Вычислительные возможности систем Продолжим наше сравнение СКМ (систем компьютерной математики) Maple 9 и Mathematica 5. Эта статья будет посвящена сопоставлению вычислительных и отчасти учебных и прикладных возможностей систем. Сразу оговоримся, что речь пойдет только о базовых поставках пакетов, поскольку функциональность обеих СКМ можно значительно расширить. Чтобы в этом убедиться, достаточно посетить web-узлы систем и просмотреть обширные списки предлагаемых пакетов расширений. Многие из них доступны для свободного распространения, но имеются и профессиональные коммерческие продукты. Применяемые вычислительные технологии Несмотря на близость функциональных возможностей двух систем, разработчики применяют в них различные вычислительные технологии. Так, некоторые функции Maple, начиная с шестой версии, включают высокоэффективные алгоритмы NAG (Numerical Algorithms Group) — ведущего мирового лидера по поставке алгоритмов и программных решений для научного ПО и визуализации данных. В девятой версии Maple это сотрудничество получило дальнейшее продолжение. Значительная часть высокоэффективных алгоритмов системы была создана при участии группы NAG, особенно операторов линейной алгебры, требующих больших затрат ресурсов и машинного времени. Другим важным новшеством стало применение библиотеки GMP (GNU Multiple Precision) для арифметики высокой точности. Библиотека GMP включает эффективные алгоритмы для арифметических операций с числами различного представления (целыми, рациональными, с плавающей точкой), которые выполняются быстрее, чем в предыдущих версиях, и требуют меньших ресурсов. Mathematica 5, в свою очередь, реализует новейшие инновационные технологии, важнейшие из которых мы кратко опишем. Весьма существенной среди новых подходов является такая возможность системы, как автоматический выбор алгоритма решения задачи. Например, если пользователю необходимо численно решить дифференциальное уравнение (команда NDSolve), право выбора наиболее подходящего алгоритма можно вполне доверить программе. Mathematica не только определит лучший (в смысле сходимости, точности и т.п.) алгоритм для данного класса уравнения, но и заменит его на другой в процессе вычисления, если какие-либо параметры промежуточных вычислений окажутся неудовлетворительными. Кроме того, анализируя входные данные решения, система постарается выдать конечный результат в наиболее адекватной форме (символьной, точной или приближенной). Для работы с арифметикой высокой точности в Mathematica применяется технология gigaNumerics, созданная специалистами Wolfram Research. Функции системы для работы с численными операциями используют адаптивный контроль точности, в соответствии с которым точность вычислений не фиксируется на протяжении выполнения алгоритма, а при необходимости регулируется. Это позволяет избежать многих известных отрицательных вычислительных эффектов (например, достижение машинного нуля), присущих приложениям, основанным на общих языках программирования, а также многим вычислительным системам. К другим ключевым возможностям технологии gigaNumerics относятся прекомпиляция (позволяет ускорить вычисления), использование упакованных массивов Packed Arrays (компактность хранения достигается благодаря специальному формату), оптимизация алгоритма под процессор (в том числе и 64-разрядный) и векторизация (возможность обработки массивов как единого целого, что позволяет применять высокоскоростные низкоуровневые процедуры доступа). Говоря о вычислительных технологиях систем, особо обратим внимание читателя на то, что многие алгоритмы (как для символьных, так и численных вычислений) не имеют каких-либо программных ограничений на величину или точность выражений, с которыми они оперируют. Таким образом, все вычисления, — по крайней мере, теоретически — в представляемых СКМ можно проводить точно (без округлений), что в некотором смысле уравнивает вычислительную математику с аналитической. Единственным реальным сдерживающим фактором при такого рода расчетах остаются аппаратные и временные ограничения. Несколько иллюстративных примеров Мы говорили, что вычислительные возможности систем имеют немало общего. По сути, идентично выполняются основные операции анализа, алгебраические преобразования, обращения к функциям. Но все-таки здесь обнаруживаются небольшие отличия. Так, в Mathematica многие команды операций анализа имеют своего численного «двойника». Например, оператор интегрирования Integrate имеет «двойника» NIntegrate, который применяется для численного интегрирования. Такое разделение операций анализа на символьные и численные обеспечивает повышенный контроль над вычислениями. В Maple для вычислений выражений реализован несколько иной подход. Операции анализа осуществляются с помощью единых операторов. Если же значение выражения необходимо получить в той или иной форме, для его вычисления используют специальную функцию, которая обычно начинается с префикса eval. Этот способ применяют для вычислений над полем комплексных чисел, булевских и матричных выражений, вычислений с плавающей точкой (с произвольной или машинной точностью). Такой механизм позволяет комбинировать различные вычислительные процедуры и проводить, например, алгебраические операции над комплексными массивами с заданной точностью. Важное место в наборе функций каждой из систем занимают операции линейной алгебры. Так, Maple содержит два пакета (linalg и LinearAlgebra), посвященные данному типу вычислений. Оба пакета поддерживают близкие линейно-алгебраические функции (примерно по сотне команд, охватывающих такие действия, как вычисление определителей, обращение матриц, представления и разложения матриц в различных формах и другие), но сфера их применения различна. Пакет linalg более предпочтителен для использования в аналитических преобразования, в то время как LinearAlgebra снабжен высокоэффективными процедурами от группы NAG, предназначенными главным образом для быстрой обработки больших численных матриц. Кроме названных, среди алгебраических средств Maple имеется еще один пакет —VectorCalculus, который служит для выполнения операций векторных полей (с его помощью можно вычислять градиенты, роторы, лапласианы и другие операторы). Mathematica имеет похожий набор инструментов, хотя конкретная организация алгебраических функций иная. Большинство алгебраических операций входят в ядро системы и вызываются без обращения к пакетам расширений. Во внешние расширения (а именно в пакет LinearAlgebra) входит относительно небольшое число функций, относящихся к операциям с матрицами (удаление/добавление блоков), ортогонализации Грамма-Шмидта, вычислениям с матрицами специальных видов и т.д. Аналогом пакета VectorCalculus в Mathematica является пакет расширений VectorAnalysis, который также предназначен для вычисления операторов векторных полей. Однако если VectorCalculus (в Maple) оперирует со встроенным типом rtable, позволяющим создавать массивы до 63 измерений, то размерность векторных полей в VectorAnalysis (Mathematica) ограничена всего тремя измерениями. В целом обе СКМ поддерживают значительное (и, видимо, даже основное) количество функций, близких или идентичных по своим возможностям. Они охватывают такие важные разделы математики, как теория чисел, дифференциальные уравнения, непрерывные и дискретные интегральные преобразования, линейное программирование, теория групп, аппроксимация, теория алгебраических кривых, вариационное исчисление и другие. Кроме математических, имеются много функций из некоторых смежных областей — статистики и финансов. Но поскольку перечисление всех возможностей заняло бы слишком много места и потребовало углубления в некоторые специальные математические вопросы, мы поступим по-другому — обратимся к образовательным и прикладным возможностям систем, которые, безусловно, интересуют многих наших читателей. Учебные средства и прикладные области В прошлой части обзора мы отмечали, что разработчики рассматриваемых СКМ большое внимание уделяют образовательным возможностям пакетов. В этой области бесспорное первенство принадлежит Maple (в случае, если речь идет о базовой поставке). В состав версии 9 входит специальный учебный пакет Student, включающий три подпакета, предназначенных для обучения студентов начальных курсов основам таких дисциплин, как введение в высшую математику, анализ функций одной переменной и линейная алгебра. Функции этих подпакетов вызывают интерактивные репетиторы, которые в простой, наглядной форме проведут пользователя по основным операциям названных дисциплин. Даже не имея никаких представлений об этих предметах, Вы легко сможете освоить базовые операции анализа и линейной алгебры. Например, функция EigenvaluesTutor наглядно продемонстрирует на экране все этапы вычисления собственных чисел матрицы (рис. 1), после чего решить очередную контрольную по алгебре для Вас будет парой пустяков :-). Mathematica, увы, подобных средств в своем распоряжении не имеет.
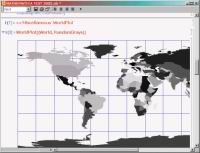
Оба пакета обладают достаточно мощными инструментами для широкого применении в прикладных областях. Начнем с Maple. Физики и химики могут воспользоваться пакетом ScientificConstants, предоставляющим доступ практически ко всем важнейшим физическим постоянным — от скорости света до характеристик элементарных частиц. С его помощью легко получить исчерпывающую информацию обо всех элементах периодической системы и их изотопах. А для перевода одних единиц измерения в другие можно воспользоваться пакетом Units, который в версии 9 приобрел графический интерфейс, позволяющий конвертировать величины без ручного введения кода. Mathematica также может быть с успехом использована прикладниками. Пакет ChemicalElements в качестве справочника пригодится химикам: кроме атомных характеристик элементов, с его помощью можно узнать их важнейшие физические свойства, например, температуру точки кипения/замерзания и даже распространенность элемента в солнечной системе, земной коре и океанах. Другой пакет —PhysicalConstants — незаменим при физических расчетах. Он содержит важнейшие физические константы, среди которых немало оригинальных (например, возраст Вселенной в секундах :-)). Географы также не были обойденными вниманием разработчиков Mathematica. Система включает несколько пакетов для работы с геодезическими и географическими данными. CityData содержит информацию о геодезических координатах крупнейших городов мира и позволяет поддерживать пользовательскую базу данных с информацией о городах. Другой пакет WorldPlot позволяет строить географические карты (рис. 2). Еще одной особенностью Mathematica, отсутствующей в Maple, является богатый набор функций для работы с цифровым звуком в пакете Audio. С его помощью можно обрабатывать файлы в формате цифрового звука и генерировать звуковые сигналы сложных волновых форм.
Подытоживая сегодняшний материал, можно сделать вывод, что в области вычислительных возможностей описываемые системы достаточно близки. Более глубокие отличия проявляются в дополнительных функциях, на что необходимо обращать внимание пользователям. Рекомендуем ещё прочитать:
|
|
|
| Хостинг на серверах в Украине, США и Германии. | © sector.biz.ua 2006-2015 design by Vadim Popov |






 Идёт загрузка...
Идёт загрузка...