АРХИВ СТАТЕЙ ЖУРНАЛА «МОЙ КОМПЬЮТЕР» ЗА 2003 ГОД

Два кита математики

• Все журналы \ Номер 48/271 `2003 от 01.12.2003 \ Два кита математики

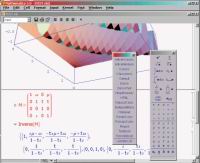
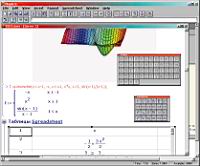
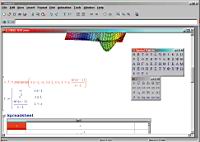
Константин НОСОВ k_n@ua.fm

Системы компьютерной математики (СКМ) находят сегодня все более широкое применение в самых различных областях науки и техники. И хотя главными пользователями этих продуктов по-прежнему остаются математики и инженеры, нередко к этим программам обращаются и представители других дисциплин — физики, химики, биологии, вплоть до исследователей в области гуманитарных наук, не говоря уже о студентах и школьниках, в среде которых эти пакеты получили заслуженное признание.

Причина широкой популярности СКМ состоит в поддержке этими приложениями универсальных средств моделирования сложных и абстрактных явлений самой разной природы. В отличие от специализированных вычислительных пакетов, ориентированных на конкретную предметную область, ведущие СКМ совмещают в одной оболочке обширный набор инструментов, позволяющий решать масштабные научные задачи. Как правило, в эти пакеты входят процедуры для численных и аналитических расчетов, средства для визуализации, программирования и представления результатов. Таким образом, пользователь получает полный набор инструментов для проведения всех этапов исследования — от реализации предварительных расчетов до составления итогового отчета.

Сегодня на рынке имеется несколько универсальных СКМ, обладающих описанными свойствами. Читателям, интересующимся компьютерной математикой, хорошо знакомы названия таких программных пакетов, как Mathcad, MuPAD, Matlab, Macsyma и других. Сравнение всех этих мощных пакетов между собой — задача очень непростая, хотя попытки такого рода и имеются (например, в обширном обзоре Computer Algebra Systems: A Practical Guide. John Wiley&Sons, 1999, 452 p.). В качестве сегодняшней темы мы выбрали сопоставление двух СКМ, представляющих передовую компьютерных технологий в этом секторе ПО. Речь идет о Mathematica 5 от Wolfram Research и Maple 9 от Waterloo Maple Inc.

Напомним, что с предыдущими версиями пакета Maple наш журнал уже знакомил читателей (смотрите обзоры автора «Maple — кленовый символ математики», МК №3 (174), «Математические пироги с кленовым сиропом», МК №10 (181)). Наш сегодняшний выбор определился следующими соображениями. Во-первых, указанные системы действительно являются наиболее мощными полнофункциональными вычислительными системами универсального назначения. Во-вторых, обе занимают практически одну и ту же нишу на рынке, что делает их сравнение уместным. В связи с этим отметим, что сегодня Mathematica и Maple практически не имеют конкурентов: другие СКМ либо заметно им уступают, либо отличаются функциональной направленностью. Наконец, совсем недавно — летом этого года — были выпущены новые версии систем, что делает выбранную тему интересной как для новичков, так и для опытных пользователей предыдущих версий.

Наш обзор мы разделили на три части. В первой рассмотрим некоторые общие вопросы, не относящиеся непосредственно к вычислительным свойствам систем, во второй сопоставим вычислительные возможности пакетов, в третьей сравним эффективность некоторых вычислительных операций на модельных примерах.

Общие свойства систем

Особенности архитектуры и связь с внешними приложениями.

Прежде чем перейти к сравнению функциональных свойств, немного расскажем об общей архитектуре описываемых систем. Обе СКМ создавались как соединение интерфейсной оболочки и ядра. Интерфейс отвечает за взаимодействие с пользователем (ввод и отображение результатов), ядро выполняет функции математического процессора, производящего вычисления. Такая двухкомпонентная архитектура имеет очевидные преимущества. Важнейшее из них состоит в том, что становится возможным разделение функций систем на основные, включенные в ядро, и дополнительные, включаемые в пакеты расширений (Add-ons в Mathematica и Packages в Maple). Функции пакетов расширений не доступны в обычном режиме работы и загружаются в память только по мере необходимости, что позволяет экономить ресурсы и способствует большей структурированности систем. Другое важное преимущество двухкомпонентной архитектуры — в возможности построения на базе ядра собственных приложений, выполняющих специфические задачи. В этом плане между Mathematica и Maple имеются заметные отличия.

Так, в поставку Mathematica входит три программных средства для поддержки взаимодействия системы с внешними приложениями — J/Link, MathLink и .NET/Link. Остановимся на их существенных свойствах.

J/Link служит мостом для соединения Mathematica с Java-приложениями. J/Link позволяет вызывать программы на Java из Mathematica и обращаться к ядру системы из внешних приложений на Java. С помощью J/Link можно загружать произвольные Java-классы в Mathematica и создавать Java-объекты, вызывать их методы и получать доступ к их полям прямо из программной среды системы. Соединение обеих технологий (Mathematica и Java) позволяет создавать принципиально новые вычислительные системы — вплоть до построения нового интерфейса, заменяющего поставляемую с продуктом стандартную оболочку.

Для соединения Mathematica с другими (не обязательно на Java) приложениями служит специальный протокол системы MathLink. Его важнейшими функциями являются управление внешними программами из Mathematica, передача данных в обоих направлениях (между Mathematica и внешней программой) и обмен данными между параллельными процессами в самой Mathematica.

Средство .NET/Link, как несложно понять, служит для соединения Mathematica с технологической платформой Microsoft .NET, заменяющей предшествовавшие ей технологии MFC, COM, ASP и другие. Не вдаваясь в тонкости, скажем, что J/Link и .NET/Link можно рассматривать как определенные расширения универсального протокола MathLink, имеющие некоторые специфические особенности.

Maple также обладает некоторыми аналогичными средствами, впрочем, не столь разнообразными. Из пакета можно получить доступ к внешним динамическим библиотекам, а для использования функций ядра Maple — воспользоваться библиотекой OpenMaple, позволяющей обращаться к системе из откомпилированных модулей на языке С.

Заметим, что названные программные средства обеих систем требуют глубокого знания программирования и обычно применяются подготовленными пользователями.

Интерфейс, издательские возможности и форматы обмена.

Впрочем, для того чтобы успешно использовать системы, не нужно быть квалифицированным программистом. Интерфейс описываемых СКМ устроен таким образом, что для эффективной работы достаточно элементарных навыков и небольшой интуиции. Основные документы систем максимально отражают особенности общепринятой математической нотации, благодаря чему практически каждый пользователь может приступить к работе без предварительной подготовки. Но и здесь между СКМ имеются некоторые различия, на важнейших из которых мы и остановимся.

Mathematica (рис. 1) поддерживает документо-ориентированный документ (document-centered interface, DCI). Согласно этому принципу, документ должен содержать основные интерактивные элементы, данные, графики, программный код и т.д. Как видно на иллюстрации, собственным окном приложения является лишь плавающая полоска меню, все остальное — основные документы системы (Notebook), инструментальные панели, окно системы помощи — представляют собой интерактивные документы стандарта DCI. Документ Mathematica состоит из ячеек, которые можно объединять в более крупные структуры. Программа обладает еще одной редкой особенностью — вид ее документа регулируется более чем пятьюстами настройками. И хотя для большинства задача такое разнообразие излишне, в некоторых случаях оно оказывается полезным.

В Maple реализован более традиционный подход к интерфейсу — последний включает обычные элементы многооконных приложений: главное окно программы с меню, строкой состояния и командными панелями. Пользователь может выбрать отображение интерфейса в классическом варианте (рис. 2), пришедшем из прежних версий, или стандартном (рис. 3), являющимся новшеством девятой версии. В частности, стандартный вариант позволяет использовать интерактивный отладчик процедур и поддерживает новый, более совершенный интерфейс справочной системы. При этом функциональные возможности интерфейсов полностью совпадают.

Из особенностей интерфейса Maple отметим развитую систему контекстного меню, благодаря которой с выражениями можно производить отвечающие их типу преобразования. Например, контекстное меню для матриц позволяет вызвать матричный редактор (Matrix Browser), выполнить основные операции линейной алгебры (подсчет нормы, собственных чисел и т.п.), конвертировать матрицу в различные внешние форматы. Для проведения данных преобразований не нужно знать синтаксис команд, достаточно выбрать нужный пункт из меню, появляющегося при нажатии правой кнопкой на выбранном объекте.

Другим важным элементом интерфейса Maple (непосредственно связанным с функциональностью и структурой документов) являются электронные таблицы Spreadsheet, которые встраиваются в документы системы наряду с другими объектами. Удобство использования таблиц, сочетающих вычислительные возможности Maple с функциями табличных процессоров, заключается в способности системы производить в единой среде сложную обработку массивов и в наглядной форме отображать результаты.

Завершая рассмотрение интерфейса, отмечу небольшой, но ощутимый недостаток Maple, унаследованный от прошлых версий: масштаб отображения документов может принимать только небольшое число фиксированных значений (50%, 75% и т.д.).

Перейдем к издательским возможностям систем. Оба пакета позволяют создавать структурированные, многоуровневые документы, поддерживающие гипертекстовые ссылки и стили оформления параграфов (в Maple имеются также стили для символов). Важной функцией систем является встроенная проверка орфографии. Но в целом различий в издательских функциях пакетов гораздо больше, чем сходства.

В этой области бесспорное первенство принадлежит Mathematica, причем даже в сравнении со всеми другими современными СКМ. Даже ранние версии этого пакета создавались как высокофункциональные издательские системы, ориентированные на подготовку публикаций, содержащих большое количество формул. Поэтому вполне закономерно, что нынешняя версия включает в себя практически исчерпывающий набор инструментов для написания математических текстов произвольной сложности и в этом отношении может на равных конкурировать с профессиональными издательскими системами для подготовки научных публикаций. Рассмотрим основные механизмы реализации этих функций.

Mathematica поддерживает около 700 математических символов, охватывающих условные обозначения из различных разделов математики. В этот набор также включены буквы нескольких алфавитов — греческого, готического и других, используемых в научных текстах. В документы можно включать формулы произвольной сложности, как строчные, так и выключные. Предусмотрена автоматическая нумерация разделов документа и формул.

Для оформления публикации в целом в системе имеется специальный пакет AuthorTools, функции которого позволяют создавать такие важные элементы, как оглавление, предметный указатель, поля для отображения плавающих параметров (дата/время и пр.), колонтитулы (эти функции применимы как к отдельному документу, так и к их группам). Для создания документов-презентаций, которые будут демонстрироваться на экране, в системе предусмотрен специальный мастер Slide Show.

Говоря о Maple, отметим, что издательские возможности этой системы заметно скромнее. Набор математических символов практически ограничен греческим алфавитом, не доступны автоматическая нумерация и генерирование упомянутых разделов документа. В целом издательские возможности пакета находятся на уровне обычного текстового процессора c включением поддержки математической символики.

Если же пользователя не удовлетворят встроенные возможности по подготовке публикаций, документы систем можно экспортировать во внешние форматы. И Maple, и Mathematica поддерживают обширные, во многом близкие экспортные возможности. Документы обеих СКМ можно сохранить в таких популярных форматах, как XML, MathML, TeX, HTML (и различных вариациях вроде XHTML, на это вопросе останавливаться не будем). Общими форматами для сохранения графики являются TIFF, GIF (обычный и анимированный), JPEG, BMP и некоторые другие. Структурированные массивы (матрицы, векторы) легко преобразуются в распространенные табличные форматы Matlab, MatrixMarket и текстовый с разделителями. Но и в этой области описываемые СКМ не совсем равнозначны. В частности, Mathematica поддерживает более широкий список графических форматов и некоторые цифровые акустические форматы, а Maple позволяет сохранять документы в RTF, недоступном в Mathematica.

Средства программирования и графические возможности.

Такие мощные системы, как рассматриваемые СКМ, обычно используют, не прибегая к программированию. Их стандартные возможности по большей части значительно превосходят реальные запросы многих пользователей, которые часто и не подозревают, что в этих пакетах можно еще и программировать :-). Но если Вы сталкиваетесь со сложными задачами, Maple и Mathematica готовы предоставить изощренные возможности программирования в своих средах. При этом программные средства систем заметно отличаются, чего мы кратко коснулись в разделе о взаимодействии с внешними приложениями.

В Mathematica используется собственный проблемно-ориентированный язык программирования сверхвысокого уровня, по своим функциональным свойствам значительно превосходящий языки общего назначения типа C или Java. Вобрав в себя лучшие качества многих языков программирования, язык Mathematica позволяет реализовывать большинство актуальных концепций программирования — объектно-ориентированное, структурное, рекурсивное и т.д. Многие операторы этого языка ориентированы на ядро системы, содержащее готовые алгоритмы, реализация которых на языках общего назначения потребовала бы написания сложных и объемных программ. Несмотря на эти достоинства, язык Mathematica немного архаичен и громоздок (по крайней мере, внешне), что затрудняет его освоение и применение.

Язык Maple в целом не предоставляет такого разнообразия концепций применения, но для массового пользователя он более предпочтителен благодаря своей простоте и изяществу. Его операторы близки к аналогичным конструкциям C, Fortran, Basic и Pascal, что облегчает освоение программирования в этой системе.

Программные средства пакетов не исчерпываются программной средой. Процедуры на внутреннем языке могут быть переведены в коды на других языках и использованы во внешних приложениях. Так, Mathematica переводит собственный код в C и Fortran; Maple, помимо этого, еще и в Java, Matlab и Visual Basic.

Графические возможности СКМ Mathematica и Maple давно стали промышленным стандартом и образцом среди других систем научной графики. Эти возможности столь широки, что даже беглое их рассмотрение требует отдельного материала. Поэтому ограничимся самой общей информацией.

Обе системы позволяют строить внушительную галерею двух- и трехмерных графиков в различных системах координат, применяя для достижения нужных эффектов большое количество параметров, относящихся к цвету, толщине линий, координатным осям, характеру заливки поверхности, источникам подсветки и т.д. Для иллюстраций динамических процессов можно создавать настраиваемые анимационные графики. Оценивая графические возможности пакетов, сложно отдать какой-либо из них предпочтение, но по личному мнению автора, графика Maple включает большее число нестандартных возможностей (графики многолистных функций, график на бесконечном интервале и т.д.) и интерактивных свойств. Если в Mathematica график практически нельзя изменить после создания, то Maple допускает тонкую настройку рисунка уже после его построения. Начинающие пользователи этого пакета могут прибегнуть к мастеру построения графиков Plot Builder, с помощью которого без лишних хлопот удастся создать сложный график, не прибегая к ручному вводу команд. В версию 9 включена поддержка графической технологии OpenViz, сделавшей графику систему более качественной и добавившей настойку прозрачности рисунков.

Завершая первую часть обзора, хочу подчеркнуть, что нам сознательно пришлось опустить некоторые важные моменты, относящиеся к заявленной теме, и выразить надежду, что разобраться с этими вопросами читатель сумеет самостоятельно.

(Продолжение следует)

Идёт загрузка...

Данную страницу никто не комментировал. Вы можете стать первым.

Ваше имя:
Ваша почта:
Комментарий:
Введите символы или вычислите пример: * Обновить