 
|
|
Новости
Статьи
Магазин
Драйвера
Контакты
RSS канал новостей
Программаторы 25 SPI FLASH
Адаптеры Optibay HDD Caddy
Драйвера nVidia GeForce
Драйвера AMD Radeon HD
Игры на DVD
Сравнение видеокарт
Сравнение процессоров
В конце марта компания ASRock анонсировала фирменную линейку графических ускорителей Phantom Gaming. ... Компания Huawei продолжает заниматься расширением фирменной линейки смартфонов Y Series. Очередное ... Компания Antec в своем очередном пресс-релизе анонсировала поставки фирменной серии блоков питания ... Компания Thermalright отчиталась о готовности нового высокопроизводительного процессорного кулера ... Компания Biostar сообщает в официальном пресс-релизе о готовности флагманской материнской платы ... |
АРХИВ СТАТЕЙ ЖУРНАЛА «МОЙ КОМПЬЮТЕР» ЗА 2003 ГОДВ графском парке
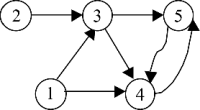
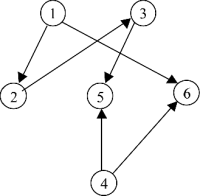
Продолжение, начало см. в МК № 33-34, 38 (256-257, 261). Часть 6. Достижимость за определенное количество шагов Углубляясь в вопрос достижимости, можно поставить перед собой задачу: выяснить, достижима ли нужная вершина именно за k шагов. Под количеством шагов мы будем подразумевать количество ребер, которые нам предстоит пройти, чтобы подобраться к вершине. Ведь на практике может случиться такое, что количество шагов ограничено, а добраться до нужного пункта таки предстоит. В науке существует такое понятие —матрица достижимостей k-го порядка. Если матрица смежностей демонстрирует нам картину достижимости той или иной вершины в виде смежностей (то есть за один шаг), то матрица достижимостей k-го порядка (k>1) гласит о существовании маршрута длиной в k ребер между вершинами i и j. Рассмотрим ориентированный невзвешенный граф:
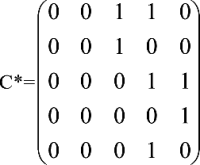
Его матрица С* имеет вид:
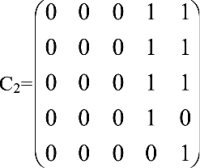
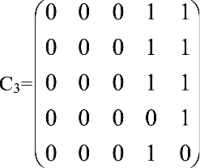
Тогда матрицы достижимостей 2-го и 3-го порядка будут выглядеть так:
Проверяем. Смотрим на матрицу С2. В ячейке С2[2,5] стоит 1. Из этого следует, что из вершины 2 существует маршрут длиной в 2 дуги (индекс матрицы) к вершине 5. Действительно, на рисунке этот путь отчетливо виден: дуги (2,3), (3,5). Или же ячейка С2[4,4]: из вершины 4 в нее же можно попасть, пройдя 2 дуги: (4,5) и (5,4). Наконец, в матрице C3 ячейка С3[1,4] показывает, что за 3 шага из вершины 1 мы достигнем вершины 4. Глядя на рисунок, проходим дуги (1,3), (3,5), (5,4). А вот из вершины 2 в вершину 3 ни за 2, ни за 3 шага не попадешь (ячейки C2[2,3] и С3[2,3] имеют значение 0), зато попадешь за 1 шаг, глядя на ячейку С* (или С1). Просто? Невероятно просто! И красиво :-)! Я почти уверен, что пытливый читатель задаст весьма своевременный вопрос: как построить эти вездесущие матрицы достижимостей (их еще называют матрицами путей)? Секрет фокуса я вам непременно открою. Надеюсь, из курса высшей математики вы знакомы с алгоритмом умножения матриц. Делается это не поэлементно, а по строчкам и столбикам. Так, если мы умножаем матрицу C саму на себя, то элементы результата (то есть матрицы С2) определяются по правилу:
Так вот, матрица C2 — это всего лишь матрица C1 в квадрате: С1*С1. А матрица С3=С2*С1 (или С1 в кубе). Тогда Сk=C1*C1*…*C1 (k-1 умножений) или С1 в k-й степени. Напишем функцию, строящую матрицу достижимостей k-го порядка и проверим достижимость вершины v из вершины p за k шагов. Эта процедура выдает нам достижимость вершины v из вершины p ровно (!) за k шагов. Если нам дано условие «не больше, чем за k» шагов, то 1 должна стоять в ячейке [p, v] хотя бы одной из матриц C1, C2, …, Ck. Часть 7. Топологическая сортировка Пускай у нас есть ориентированный граф, который не содержит циклов. Ставится задача: обойти вершины граф таким образом, чтобы меньшая вершина в этом обходе посещалась позже, чем бо[ударение!]льшая. Вы не подумайте, что бо[ударение!]льшая вершина — это вершина с бо[ударение!]льшим номером. Пускай на графе вводится отношение частичного порядка. А именно: вершина А считается меньше вершины В, если в графе есть дуга (А,В). Приведем пример из жизни. Около года назад ваш покорный слуга проходил медосмотр для получения водительской медицинской справки. На лекцию по оказанию первой медицинской помощи на дорогах нельзя было попасть без предварительного обследования у психиатра, нарколог не принимал до тех пор, пока не получишь справку о прослушивании лекции, и только потом можно было идти к офтальмологу, невропатологу и т.д. В этом случае мы имеем дело с топологической сортировкой. Требуется проходить вершины (пункты приема) графа таким образом, чтобы конец любой дуги предшествовал ее началу. Важной является следующая деталь: орграф не может содержать циклов. Кроме того, из некоторых вершин может выходить/входить несколько дуг. Проиллюстрируем вышесказанное:
При топологической сортировке порядок обхода графа будет следующим: 5, 3, 2, 6, 1, 4. Для построения алгоритма решения нашей задачи несколько видоизменим поиск в глубину: Идея алгоритма состоит в том, что вызов подпроцедуры Inside(i) посещает все вершины, большие i (достижимые из i). После обработки всех вершин, достижимых из i, все до сих пор непосещенные вершины не могут быть больше i, поскольку: а) они были пройдены до вызова Inside(i); б) они были пройдены в процессе этого самого вызова. Следовательно, вершина i больше оставшихся, ее и выводим. Часть 8. Подграфы Представьте себе любой город. Город Киев, например. Его можно схематически представить в виде графа: улицы — это последовательность ребер, перекрестки — вершины. Мы также замечали, что улицы бывают с односторонним и двусторонним движением, что влияет на ориентацию графа. Пусть G — граф, который является моделью нашего города. Так повелось, что каждый город административно-территориально делится на районы, те в свою очередь на массивы (микрорайоны), и т.д. Аналогично можно рассуждать, взяв в пример целую страну. Области, районы — ее составляющие. Для чего я все это рассказываю? Дело в том, что мы с вами сейчас поговорим о подграфах. Подграф графа G — это граф K, который содержит некоторые вершины и ребра графа G. Заметим, что подграф может и не содержать ребер. Любая вершина графа G уже является подграфом. Что касается ребер, то они обязательно должны содержать обе свои инцидентные вершины:
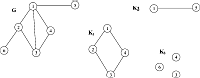
Такой граф не будет подграфом, так как ребро подразумевает как свое начало, так и конец. Давайте приведем примеры подграфов:
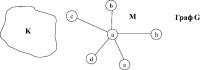
K1, K2, K3 — подграфы графа G. Конечно, эти подграфы могут не отвечать областям или районам. Области, районы — это частные случаи. Как проверить, является ли один граф подграфом другого? Пускай граф задан списком ребер. Идея довольно простого метода следующая: проверить вхождение одного списка ребер в другой. Делается это посредством прохождения меньшего (по количеству элементов) списка и отыскиванием его текущего элемента в другом (большем) списке. Если такого элемента не существует, ответ сразу же отрицательный: данный граф не является подграфом другого графа. Алгоритм закачивает работу и выдает результат в тех случаях, когда мы нашли «лишний» элемент в меньшем списке, или когда весь список пройден и «лишних» элементов не обнаружено. Можно поступить и по-другому: удалять совпавший элемент из меньшего списка, и после того как больший список будет пройден, проверить: является ли меньший список пустым. Если является, то результат положительный: первый граф является подграфом второго. Если непустой — значит, есть «лишний» элемент, и ответ, соответственно, отрицательный. Запишем программный код первого способа: А теперь второй способ: Давайте теперь рассмотрим пару задачек о подграфах, которые не вписываются в условия вышеизложенных. Поставим перед собой цель: выяснить, есть ли в данном графе изолированный подграф в виде звездочки с k лучами? К примеру, для k=5 выглядит это приблизительно следующим образом:
На рисунке граф G представляет собой объединение (грубо говоря, сумму) двух своих изолированных подграфов: графа K и графа M. К слову, M как раз и будет той «звездочкой», о которой мы говорим, — с пятью лучами. Для решения задачи будем использовать такой алгоритм: 1. Пускай на входе есть список смежностей ListOfAdjacencies в виде массива массивов записей. 2. Просматриваем все вершины и находим такие, которые имеют k смежных. Пускай вершина i имеет k смежных вершин. 3. Просматриваем каждую вершину, смежную с i. Если каждая из них имеет только одну смежную (разумеется, это будет вершина i), то результат положительный: изолированный граф в виде звездочки с k лучами в данном графе существует. Если такой вершины i не существует, ответ отрицательный. Переведем все это на язык, понятный компьютеру: Вот и все на сегодня. Если последняя процедура показалась вам уж больно простой, не разочаровывайтесь — попробуйте отыскать в графе изолированный подграф в виде звезды с израильского флага или кремлевской, учитывая, что в каждую вершину входит 2 ребра. Или же подберите себе другую фигуру по вкусу, чтобы ощутить всю прелесть этой жизни, просидев над решением задачи несколько часов, дней, месяцев :-). (Продолжение следует) Рекомендуем ещё прочитать:
|
|
|
| Хостинг на серверах в Украине, США и Германии. | © sector.biz.ua 2006-2015 design by Vadim Popov |






 Идёт загрузка...
Идёт загрузка...