 
|
|
Новости
Статьи
Магазин
Драйвера
Контакты
RSS канал новостей
Программаторы 25 SPI FLASH
Адаптеры Optibay HDD Caddy
Драйвера nVidia GeForce
Драйвера AMD Radeon HD
Игры на DVD
Сравнение видеокарт
Сравнение процессоров
В конце марта компания ASRock анонсировала фирменную линейку графических ускорителей Phantom Gaming. ... Компания Huawei продолжает заниматься расширением фирменной линейки смартфонов Y Series. Очередное ... Компания Antec в своем очередном пресс-релизе анонсировала поставки фирменной серии блоков питания ... Компания Thermalright отчиталась о готовности нового высокопроизводительного процессорного кулера ... Компания Biostar сообщает в официальном пресс-релизе о готовности флагманской материнской платы ... |
АРХИВ СТАТЕЙ ЖУРНАЛА «МОЙ КОМПЬЮТЕР» ЗА 2003 ГОДЕго Величество Случай
Если спросить у неспециалиста, что такое случайные числа, вряд ли мы получим толковый ответ. Лишь немногие вспомнят знакомые со школы или ВУЗа понятия «random» или «RND» — пожалуй, не более того. Давайте попробуем разобраться. Случайные числа используются в компьютерных системах очень давно. Их применяют для нужд шифрования, моделирования физических процессов, проведения математических исследований. В статье мы остановимся на проблемах защиты информации. Для шифрования сообщений, например, можно воспользоваться методом гаммирования или, другими словами, наложения. Отправитель инициализирует свой ГСЧ (генератор случайных чисел) начальным значением, которое одновременно является секретным ключом. ГСЧ начинает вырабатывать по заложенному в него алгоритму случайные числа. Остается по некоторому закону наложить их на искомое сообщение, и можно отправлять адресату. Тот получает зашифрованное сообщение, которое нужно дешифровать — для этой цели понадобится секретный ключ, известный ему как законному получателю. ГСЧ получателя (такой же, как у отправителя) вырабатывает ту же самую последовательность случайных чисел, при наложении которой на шифровку можно получить исходное сообщение. Этот метод основывается на двух особенностях: 1) ГСЧ вырабатывает одну и ту же последовательность при инициализации его одним и тем же ключом — такие генераторы называются псевдослучайными — ПСЧ); 2) обратимость операции наложения — обычно это операция XOR, то есть побитовое исключающее ИЛИ (0 и 0, а также 1 и 1 дают 0, а 1 и 0 дают 1). Наложив на информацию одну и ту же гамму дважды с помощью XOR, получим исходное сообщение. Рассмотрим пример. Пусть исходное сообщение — русское слово из трех букв «МК!» (ограничимся нормативной лексикой :-)). В ASCII-коде, кодировка win-1251, оно записывается как 204, 202, 33, или в двоичном виде 11001100, 11001010, 00100001. Пусть секретный ключ —23 (выбираем произвольно), в двоичном виде 00010111. Теперь важный момент: нужно определить, какой тип ПСЧ мы используем. Довольно часто применяют ПСЧ типа
Xi+1=(AXi+B)modmaxX
(т.н. конгруэнтный датчик), где a, b — некоторые константы, а МАХх — верхняя граница диапазона генерации. Примем а равным 123, b равным 12345, МАХх = 255. х1 = 23 (секретный ключ, использующийся для инициализации ПСЧ), тогда х2 = (123*23+12345) mod 255 = 129, x3 = (123*129+12345) mod 255 = 162 (вычисления можно проделать в стандартном калькуляторе Windows). В двоичном виде х1 = 00010111, х2 = 10000001, х3 = 10100010. Записываем побитно исходное сообщение, а под каждым битом — соответствующий бит гаммы, в третьей строчке пишем результат побитного XOR:
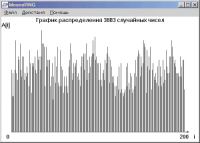
Получаем следующую двоичную последовательность: 11011011, 01001011, 10000011. Это соответствует кодам ASCII 219, 75, 131. В символьном виде это ЫКѓ. не правда ли, непохоже на «МК!» :-)? Проделайте еще раз те же операции, и вы получите исходный текст. Думаю, принцип шифрования гаммированием понятен (почему после двух наложений гаммы получается исходный текст, должно быть ясно, если разобраться с операцией XOR). Но вернемся к первоначальной теме статьи: рассмотрим более подробно работу ПСЧ. Понятно, что такой вид шифрования возможен потому, что ПСЧ дает одну и ту же гамму, если его инициализировать определенным значением (представьте, как бы мы расшифровали шифровку, если бы была сгенерирована другая гамма?) Получается, что вся гамма зависит только лишь от начального значения х1. Это, конечно, неприемлемо. Таким образом, имеем противоречие. С одной стороны, необходима однозначность гаммы для того, чтобы ее мог дешифровать законный получатель, а значит, она зависит только от одного начального инициализирующего значения ПСЧ (секретного ключа). С другой стороны эта зависимость только от начального значения позволяет злоумышленнику, подбирая начальное значение, строить всю гамму, т.е. уменьшается криптостойкость. Практически такое противоречие разрешается тем, что размер ключа увеличивается и делается равным размеру всего сообщения (т.е. размер х1 в битах равен размеру текста или файла), а значит, метод пригоден только для передачи коротких сообщений. К ПСЧ предъявляют ряд требований. В первую очередь, распределение должно быть приближено к равномерному. Это означает, что чисел в диапазоне от а до b должно генерироваться столько же, сколько от c до d (a, b, c, d — произвольные числа, принадлежащие интервалу генерирования). Иначе злоумышленник может с более высокой вероятностью предсказать генерируемые числа и раскрыть гамму. К примеру, известно, что каждое второе число генерируемое ПСЧ — двойка, а остальные числа генерируются с приблизительно одинаковой частотой. Тогда можно с вероятностью 50% предположить, что любое число гаммы — двойка, и после проверки двух чисел мы уже вряд ли ошибемся. Необходимо использовать ПСЧ с наибольшей длиной периода. Поясним, что это такое, на примере рассмотренного выше конгруэнтного генератора. Подумайте, что будет, если на определенном шаге ПСЧ выдаст число, которое уже было ранее сгенерировано? Далее он просто будет выдавать повторяющуюся последовательность чисел, т.е. зациклится. Естественно, повтор гаммы крайне нежелателен. Числа в гамме должны быть связаны минимально — так, чтобы, зная участок гаммы, нельзя было найти остальное. Конгруэнтный датчик в этом отношении плох, если известны коэффициенты a и b. Стандартный датчик, встроенный в язык программирования, вообще не рекомендуется, так как его формула известна всем. Итак, рассмотрели применение, основные требования и особенности генераторов псевдослучайных чисел. Далее рассмотрим генераторы настоящих случайных чисел. Для чего нужны ПСЧ и где их используют, мы в общих чертах разобрались. Но давайте подумаем: всегда ли нас устраивают псевдослучайные числа? Существует большое количество криптографических протоколов, в которых все ключи вычисляются на основании первоначальных базовых чисел. Возьмем RSA — там секретный и открытый ключи вычисляются на основе простых чисел p и q. Если эти числа предсказать, то ключи становятся известны автоматически. Таким образом, так как эти числа первоначально выбираются по какому-либо закону (чем ближе он к случайной выборке из множества простых чисел, тем лучше), его можно проанализировать и предсказать. А значит, злоумышленник еще до внедрения ключей в систему может предсказать их. Рассмотрим также программу генератора паролей (принципиально схожа с генератором ключей для двухключевых систем шифрования). Зная особенности ПСЧ, злоумышленник может постараться предсказать сам пароль, либо значительно уменьшить количество перебираемых вариантов. Естественно, такие ситуации недопустимы, а значит, использовать ПСЧ нельзя. Каков же выход? Выход в том, чтобы использовать генераторы случайных чисел в прямом смысле этого слова. Для этого в системе генерации должен присутствовать какой-либо элемент, вносящий случайность. К примеру, в некоторых моделях материнских плат есть встроенные аппаратные генераторы случайных чисел. Это могут быть электронные элементы, дающие белый шум на выходе (p-n переходы, либо лампы). Усиленный и оцифрованный, этот шум дает абсолютно случайное, да еще и равномерное (в определенном диапазоне, зависящем от АЧХ элемента) распределение, имеет бесконечный период и никогда не повторяется. Из других случайных физических величин часто называют скорость ветра и характеристики радиоактивного распада, но вряд ли найдется много пользователей, которые захотят устанавливать в системный блок радиоактивный элемент или подключать его к мельнице :-). Следовательно, нужно искать другие элементы, вносящие случайность. И таким элементом является сам пользователь! Да-да, ведь мы взаимодействуем с ПК посредством устройств ввода-вывода. Так, во многих книжках по криптографии мне встречалось описание программ, в которых пользователя просят набрать на клавиатуре какой-нибудь текст. Программа отслеживает интервалы в миллисекундах между нажатиями на кнопки и на их основе генерирует случайные числа. Разберем этот метод. Числа будут действительно случайно распределены, но не равномерно. Это распределение будет зависеть от конкретного набираемого текста. Так как у каждого пользователя есть свой уникальный «почерк», можно с достаточной вероятностью предсказать последовательность интервалов между нажатиями, а значит, и саму сгенерированную последовательность. Кроме того, интервалы между нажатиями вряд ли будут больше секунды (1000 мс), а минимальный интервал, который можно отследить, равен 25 мс (пусть даже 1 мс с применением особых ухищрений). Тогда может быть сгенерировано только лишь 40 (ну, пусть даже 1000) случайных чисел. Конечно, этого мало, хотелось бы больше. Больше случайных чисел! (Считайте меня маньяком случайных чисел :-)). Размышляя в этом направлении, я написал программу, которая генерирует случайные числа по перемещению мыши пользователем. Исходный текст и экзешник можно взять здесь: http://givi23.narod.ru/mouserng.rar. Программа написана на Visual C++ и использует WinAPI (около 40 Кб) — см. Рис. 1.
Каков же принцип ее работы? Пользователь водит мышью в окне программы, а координаты курсора и направление перемещения мыши дают случайный элемент. Диапазон генерирования можно изменять. Если верхняя граница меньше 1000, то координаты складываются (х+у), и к ним прибавляется направление перемещения мыши (производная от у по х). Результат берется по модулю от верхней границы (если верхняя граница больше 1000, используется другая формула для генерации). Все сгенерированные числа отражаются на графике распределения, и пользователь может интуитивно управлять процессом генерации, восполняя недостаток определенных чисел (т.е. приближать распределение к равномерному). Полученную последовательность чисел можно сохранить в обычный текстовый файл для дальнейшего использования в других целях. Проанализируем работу данной программы. Относительная равномерность распределения может быть легко достигнута путем перемещения мыши в «нужных» местах (интуитивно, думаю, понятно — стоит попробовать). Ясно, что последовательность не слишком связана, так как координаты передаются не сразу после перемещения мыши на один пиксель, а через несколько пикселей. За это время координаты успевают существенно измениться, да и последовательность их слабо предсказуема. Кроме того, направление перемещения курсора вносит дополнительный элемент случайности. Самое важное — возможность генерации случайных чисел в пределах до 1000000 (зависит от разрешения экрана). Программу можно доработать под свои нужды (исходники доступны), либо попросить об этом меня. Итак, мы рассмотрели ГСЧ: их применение в современных компьютерах, требования и принципы генерирования. Подумайте на досуге над этой проблемой и постарайтесь выдумать свой собственный ГСЧ. Если вам удастся реализовать действительно хороший генератор, возможно, у вас его даже купит какая-нибудь фирма, занимающаяся разработками в области криптографии. Ну а пока учитесь, и пусть в вашей жизни будет больше хороших случайностей — и да преследует вас удача! Рекомендуем ещё прочитать:
|
|
|
| Хостинг на серверах в Украине, США и Германии. | © sector.biz.ua 2006-2015 design by Vadim Popov |






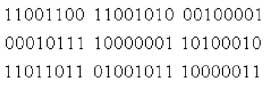
 Идёт загрузка...
Идёт загрузка...