АРХИВ СТАТЕЙ ЖУРНАЛА «МОЙ КОМПЬЮТЕР» ЗА 2003 ГОД

Японские узоры

• Все журналы \ Номер 19/242 `2003 от 12.05.2003 \ Японские узоры

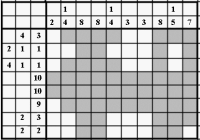
Владимир ТКАЧУК vova.tkachuk@ua.fm

Японские кроссворды — популярные и увлекательные головоломки. Многие люди любят их как вид интеллектуального развлечения, как повод проявить свои логические способности. У опытного «решателя» имеется огромный арсенал приемов для решения различных вариантов головоломки. Но программисту не менее интересно будет написать универсальную программу, разгадывающую все такие кроссворды.

С точки зрения науки...

Японский кроссворд — это матрица, состоящая из закрашенных и не закрашенных клеточек. Подряд идущие закрашенные клеточки образуют так называемые группы или последовательности. Причем, для каждой строки и каждого столбца матрицы известно, сколько групп в этой строке или столбце, в каком порядке они идут и сколько закрашенных клеточек в каждой такой группе. Между любыми рядом стоящими группами в строке или столбике находится хотя бы одна незакрашенная клеточка. Решением кроссворда считается построение такой матрицы, в которой каждый столбик и каждая срока удовлетворяли бы соответствующим описаниям (Рис. 1). В принципе, головоломка может иметь довольно много решений, а может и не иметь их вообще. Но чаще всего японские кроссворды имеет ровно одно удовлетворяющее условию решение, т.е. по заданному описанию строк и столбцов можно построить ровно одну матрицу.

Работаем «по-людски»

Человека, который много занимался решением японских кроссвордов и меньше программированием, может привести в ужас сама мысль о том, чтобы запрограммировать все возможные и необходимые, по его мнению, стратегии решения этой головоломки. О том, что бы думал программист, незнакомый с принципами решения кроссвордов, поговорим позже — интерес ведь в первую очередь представляет решение, основанное на естественной человеческой логике разгадывания головоломок. Рассмотрим, к примеру, как бы человек разгадывал кроссворд, изображенный на Рис. 1. Очевидно, что 4-я и 5-я строчки должны быть полностью закрашены. Это, в свою очередь, дает нам группу из двух клеточек в 1-м столбике; отсюда следует, что все остальные клеточки 1-го столбика не могут быть закрашенными. После этого мы можем точно определить раскраску клеток в 6-й и 3-й строках...

Не будем углубляться в тонкости «ручного» решения, а то можно за деревьями не увидеть леса. Главное — понять принцип: мы можем полностью или частично определить расположение некоторых групп, а также выявить клеточки, которые не могут быть закрашенными. Исходя из этого можно сделать еще кое-какие выводы — и так далее, пока не разгадаем весь кроссворд. Если же в процессе разгадывания мы придем к логическому противоречию, к примеру, такая-то клеточка должна быть одновременно закрашенной и не закрашенной, значит, входные данные были некорректны, т.е. решения у такой головоломки нет. Кроме того, можно еще зайти в «логический тупик», но о грустном поговорим немного попозже.

Итак, что же позволяет делать эти логические выводы в процессе решения? Дело в том, что группы в строках или столбиках не могут располагаться как попало. Иногда при всех возможных размещениях групп в столбике или строке некоторые клеточки всегда остаются закрашенными, а некоторые же, напротив, не бывают закрашенными никогда. Это дает нам право смело причислять эти клетки к закрашенным или, наоборот, к тем, которые нельзя закрашивать. В общем, если программа будет работать, руководствуясь вышеописанными принципами, то процесс решения ею кроссвордов немногим будет отличаться от аналогичного процесса, производимого человеком.

Общий язык

Чтобы не оговаривать каждый раз, что мы имеем в виду (строку или столбик), далее будем называть и то и другое просто линией. Теперь, для лучшей алгоритмизации мысли, введем некоторые определения: допустимым состоянием линии называем такое размещение групп клеточек в ней, при котором: а) все группы находятся в пределах линии; б) между каждыми рядом стоящими группами есть хотя бы одна еще не закрашенная клеточка; в) все уже закрашенные клеточки принадлежат каким-то группам; г) все клетки, которые нельзя закрашивать, находятся вне групп. То есть, допустимое состояние — это вариант расположения групп в линии, который на текущий момент может претендовать на решение. Тогда допустимым расположением конкретной группы в линии назовем такое расположение, при котором возможно допустимое состояние самой линии.

Теперь можем сделать некоторые утверждения: если в линии есть клеточка, которая принадлежит какой-то группе во всех допустимых положениях этой группы, то она вне всяких сомнений является закрашенной, напротив, если клеточка не принадлежит ни одной группе ни в одном допустимом положении, то она не должна закрашиваться. Определить клеточки, которые должны быть закрашенными, очень просто: эти клеточки принадлежат пересечению самого левого (верхнего) допустимого положения группы и самого правого (нижнего).

Сложнее определить само множество допустимых положений данной группы. Будем искать допустимые положения правой (верхней) клеточки группы, так как она вместе с длиной группы (которая известна из условия) фиксирует саму группу. Первая клеточка конкретной группы должна размещаться так, чтобы все предшествующие и последующие группы могли уместиться в линии — это дает нам первое ограничение на поиск допустимых положений клеточки. Далее, при правильном положении группы части линии до и после этой группы должны находится в допустимых состояниях. Сначала можно искать множество таких допустимых положений, при которых часть линии до группы находится в допустимом состоянии; потом — множество таких, при которых с линией после группы тоже все в порядке. Пересечение двух найденных множеств и будет искомым множеством допустимых положений группы.

От разговоров к делу

Теперь мы можем приступать к самому алгоритму решения головоломки. На словах он очень прост: следует поочередно проводить поиск допустимых состояний групп в строках и столбиках, закрашивать или помечать не закрашенными некоторые клеточки, продолжать действие до... Ну, признаков завершения работы три: кроссворд полностью разгадан, найдена ошибка в условии или программа зашла в логический тупик. Немного подумав, можно установить, что первый и третий признак принципиально не отличаются, и проявляются они тогда, когда программа не может более определить состояние ни одной новой клеточки. Ошибка в условии обнаруживается, если множество допустимых положений такой-то группы пусто, в то время как для решения задачи оно должно содержать хотя бы одно положение группы. Теперь вашему вниманию предлагается фрагмент программного кода на языке Pascal:

Головокружение от успехов

Представленная программа (конечно, если дописать ее до конца) решила большинство из предложенных тестовых кроссвордов. При размерах матрицы вплоть до 5050 время работы никогда не превышало нескольких секунд. При этом программу можно оптимизировать еще и еще. Например, можно не просчитывать множества каждый раз заново, а запоминать их. Тогда мы избегаем многократного просмотра одних и тех же неподходящих позиций. Тут было бы удобно использовать структуру динамических списков вместо типа Set. Кроме того, можно было бы просматривать не все строки и столбики, а только те, в которых произвелись изменения. Но эти оптимизации сделали бы программу более громоздкой, я же, напротив, как мог, пытался уменьшить, вырезая из нее несложные, на сой взгляд, части. Основной же недостаток представленного решения в том, что такая программа может разгадать не все варианты головоломки. В первую очередь это касается кроссвордов, у которых больше одного правильного ответа. Например, существует 120 матриц, удовлетворяющих кроссворду на Рис. 2, из них программа не найдет ни одного. Возможны также кроссворды с единственным решением, для которых этот алгоритм определит не более 10% закрашенных клеточек перед тем как зайдет в «тупик».

Не одним перебором...

Некоторые кроссворды не решаются без перебора. Так, когда задачка о решении этой головоломки была предложена на международной олимпиаде школьников по информатике, то в виду ограничений (матрица не больше 88) подразумевалось переборное решение. Однако переборы бывают разные. Простой перебор предполагает закрашивания некоторых клеточек, а после — проверку на соответствие полученной картинки условию. Для простого кроссворда с «паровозиком» (Рис. 1) нужно закрасить 56 клеточек из 80, в то время как простой перебор должен будет рассмотреть ? 1.6*10^20 вариантов раскраски. То есть, время работы, учитывая высокую скорость современных ПК, будет сравнимо с периодом, истекшим с рождения первого динозавра. Куда лучшие показатели дают так называемые «умные переборы»: можно сразу закрасить клеточки в каждой строке так, чтобы они образовывали нужные группы, а затем просто двигать эти группы. Если при этом одновременно следить за тем, чтобы в каждом еще не достроенном столбике все сходилось, то можно достигнуть неплохого результата. Такой перебор быстро решает кроссворды размером до 3030, и ни какой «логический тупик» ему не грозит.

Почти как люди

Основная проблема представленного алгоритма в том, что он может зайти в тупик: кроссворд еще не разгадан, но никаких новых выводов сделать нельзя. Человек в такой ситуации, начал бы строить предположения. Так почему бы программе не поступать так же? Как только алгоритм зашел в логический тупик, он должен выбрать какое-то допустимое положение группы и предположить, что это ее точное расположение. Далее нужно закрасить или пометить как незакрашенные определенные клеточки и продолжать действовать дальше. Если в этом случае мы наткнемся на противоречие, это будет означать, что сделанное нами предположение было неверным, значит, нужно вернуться на шаг назад и сделать какое-то другое предположение. Такой подход к задаче, во-первых, максимально приближает решение к человеческой логике, а во-вторых, учитывая вычислительную скорость компьютера, позволит быстро решить любые кроссворды.

P.S. Программа, части которой опубликованы в этой статье, действительно работает, так что вы смело можете доделать ее до конца; все вышеописанные методы также вполне реально запрограммировать.

Идёт загрузка...

Данную страницу никто не комментировал. Вы можете стать первым.

Ваше имя:
Ваша почта:
Комментарий:
Введите символы или вычислите пример: * Обновить