АРХИВ СТАТЕЙ ЖУРНАЛА «МОЙ КОМПЬЮТЕР» ЗА 2003 ГОД

Вычислительная геометрия

• Все журналы \ Номер 8/231 `2003 от 24.02.2003 \ Вычислительная геометрия

Владимир ТКАЧУК vova.tkachuk@ua.fm

У среднестатистического гражданина сочетание слов «геометрия» и «компьютер» вызывает, как правило, ассоциацию с компьютерной графикой. Действительно, графика — наиболее наглядное применение геометрических принципов в компьютере. Однако помимо графики геометрический аппарат имеет огромное количество не менее важных сфер применения. На современном компьютере ставятся задачи, решение которых требует не просто нескольких формул, а достаточно сложных алгоритмов. С некоторыми из них вы познакомитесь в этой статье.

Для начала договоримся, как геометрические объекты будут представляться в памяти компьютера. Итак, точка — это пара чисел (координат X и Y). Отрезок — это пара точек, а многоугольник — это N точек; подразумевается, что они последовательно соединены отрезками, причем последняя точка также соединена с первой.

Нахождение наименьшего расстояния между точками

Такая задача может возникнуть, например, в системе контроля над транспортом: полезно знать, насколько близко транспортные средства находятся друг к другу. Кроме того, она часто встречается в задачах планировки и прокладывания маршрута. Для ее решения существуют несколько алгоритмов. Самый простой и очевидный — это перебрать расстояния между всеми возможными парами точек и выбрать из них наименьшее. Реализация не представляет особых сложностей:

Несмотря на простоту, этот метод является довольно медленным, так как приходится перебирать все N(N-1)/2 пар точек, соответственно, сложность работы алгоритма —O(N2).

Алгоритм можно существенно ускорить, если использовать геометрические соображения. Применим к задаче принцип «разделяй и властвуй».

Проведем вертикальную прямую, такую, что слева и справа от нее лежит одинаковое количество точек (если какие-то точки лежат на самой прямой, то распределим их в обе части так, чтобы в каждой получилось приблизительно поровну).

Найдем наименьшее расстояние между точками в каждой половинке (используя этот же метод).

Найдем наименьшее расстояние между точками из «пограничной зоны» — теми, которые лежат достаточно близко к разделяющей прямой с обеих сторон.

Наименьшее из найденных чисел и будет искомым минимальным расстоянием.

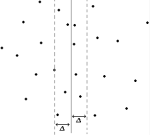
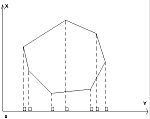
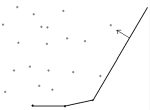
Следует отметить, что деление мы проводим только если точек больше трех, иначе ищем минимальное расстояние непосредственным перебором. Так как алгоритму придется много раз разбивать точки на группы вертикальной прямой, то целесообразно хранить точки отсортированными по X-координате, тогда разделение точек будет эквивалентно разделению массива на две равные части. Самая тонкая часть алгоритма — поиск наименьшего расстояния между точками в «пограничной зоне». Для начала, определимся, что считать «пограничной зоной». Если на текущий момент минимальное найденное расстояние ?, то рассматриваем все точки, лежащие ближе чем на ? от разделяющей прямой. Значит, «пограничная зона» — это полоска шириной в 2? (Рис. 1). Теоретически, все точки могут лежать в этой полоске, но рассматривать нужно далеко не все их пары. Из геометрических соображений становится ясным, что для каждой точки из «пограничной зоны» нужно рассматривать еще всего лишь семь таких точек, тогда будет рассмотрено около 7N пар, что конечно же меньше, чем N2. На самом деле, для выбранной точки эти семь точек можно получить, упорядочив все точки «пограничной зоны» по возрастанию Y-координаты, они будут следовать непосредственно за выбранной точкой. Для того чтобы много раз не проводить упорядочивание, можно один раз отсортировать точки по Y-координате, а после просто выбирать те, что принадлежат «пограничной зоне» из уже отсортированного множества. Оценим скорость работы алгоритма: если T(N) — время работы программы для N точек, то верно равенство T(N)=2T(N/2)+O(N) (решение задачи разбивается на решение двух меньших подзадач плюс время на объединение решений). Решением данного уравнения является T(N)=O(Nlog2N), т.е. задача работает за линейно-логарифмическое время от размера входа, что намного меньше, чем время работы простейшего алгоритма. Конечно, нужно учитывать еще и затраты на сортировку точек по X- и Y-координатам, но если сортировать методом «двоичной кучи» или «слиянием», т.е. за O(Nlog2N), то на общем времени работы это отразится мало. Реализация этого алгоритма довольно громоздка (поэтому она и не представлена в данной статье) и требует много дополнительной памяти, так что его следует применять только тогда, когда приходится иметь дело с достаточно большим количеством точек (тогда выигрыш в скорости наиболее существенен).

Вычисление площади многоугольника

Эта задача актуальна не только для домашних работ по геометрии :-), но и для приложений, связанных с планировкой или разделом чего-либо (например, земельных участков). Решений может быть несколько: можно разбить многоугольник на фигуры, площадь которых легко считается (например, на треугольники). Но если многоугольник не выпуклый, то такое разбиение само по себе — задача не из легких. Рассмотрим не столь очевидный, но намного проще реализуемый метод. Предположим, что все точки нашего многоугольника лежат выше координатной оси Ox. Тогда каждая сторона многоугольника задает прямоугольную трапецию с вершинами в ее, стороны, концах и проекциях этих концов на прямую Ox (Рис. 2). Будем считать площадь этой трапеции положительной, если левый конец отрезка находится раньше в порядке обхода вершин многоугольника, чем правый, иначе — отрицательной. Тогда площадь трапеции можно посчитать как S = (x2-x1)*(y1+y2)/2, где (x1,y1) — координаты начального конца, (x2,y2) — координаты последующего. Из геометрических соображений можно установить, что площадь всего многоугольника будет равняться модулю суммы площадей всех таких трапеций. Из тех же соображений становится понятно, почему данный метод подходит для любых многоугольников (не только тех, что выше прямой Ox). Программа, вычисляющая площадь по этому методу, очень проста:

Так как каждая сторона рассматривалась в процессе работы ровно один раз, то время работы программы —O(N). Заметим также, что площадь каждой рассматриваемой трапеции является по сути интегралом, т.е. метод сработает, даже если вершины многоугольника будут соединять не прямые отрезки, а кривые линии, интеграл которых мы можем посчитать.

Построение выпуклой оболочки

Также довольно часто встречающаяся задача: построение выпуклого многоугольника, вершинами которого являются точки из данного множества, причем все точки этого множества лежат в середине или в вершинах этого многоугольника. Другими словами, нужно построить выпуклый многоугольник наименьшей площади, покрывающий все заданные точки. Рассмотрим решение, которое вытекает из физических соображений. Пускай в пол забито N гвоздей; начнем обвязывать их веревкой, строя выпуклую оболочку. Сначала привяжем веревку к самому нижнему левому гвоздю, он-то точно принадлежит выпуклой оболочке. Далее начнем поворачивать веревку (Рис. 3) против часовой стрелки, пока не наткнемся на еще один гвоздь. Такими поворотами обвяжем все гвозди-вершины выпуклой оболочки. Правильность данного подхода практически очевидна, но как реализовать его программно? Очень просто, если сообразить, что каждый раз новое положение веревки отклоняется от старого на минимальный угол.

Положим, что сначала веревка проходила горизонтально. Тогда новую точку выпуклой оболочки следует выбирать такой, чтобы угол между новым и старым положением веревки (сторонами многоугольника) был наименьшим из возможных. Для того чтобы не загружать компьютер вычислением углов, воспользуемся векторной алгеброй (вектором будем называть направленный отрезок из точки (0;0) в точку (x;y)). Нормалью векторной пары a=(x1;y1) и b=(x2;y2) будем называть выражение x1*y2-y1*x2; известно, что оно положительно, если для того чтобы перейти от вектора a к вектору b нужно двигаться против часовой стрелки, иначе — отрицательно. Тогда угол между вектором (x0;y0) и вектором (x1;y1) меньше, чем угол между (x0;y0) и (x2;y2), если x0*y1-y0*x1?0 и x1*y2-y1*x2?0 (заметим, (x1;y1) лежит между векторами (x0;y0) и (x2;y2)). Теперь реализовать метод совсем просто:

Время работы программы есть O(NH), где H — количество вершин выпуклой оболочки. Очевидно, что это не больше O(N2), на практике же алгоритм редко когда работает дольше O(Nlog2N).

Цель статьи полагалась в том, чтобы ознакомить вас с некоторыми достижениями computer science в области геометрии. Комбинация геометрии с алгоритмами сортировки и выбора позволяет находить эффективные решения для большинства задач. Причем, методы решений актуальны и в пространственных задачах. Доказать корректность всех приведенных выше алгоритмов несложно; желающие могут заняться этим самостоятельно.

P.S. Все программы проверены на работоспособность — надо только вставить код ввода и вывода вместо троеточий :-).

Идёт загрузка...

Данную страницу никто не комментировал. Вы можете стать первым.

Ваше имя:
Ваша почта:
Комментарий:
Введите символы или вычислите пример: * Обновить