АРХИВ СТАТЕЙ ЖУРНАЛА «МОЙ КОМПЬЮТЕР» ЗА 2002 ГОД

Математические пироги с кленовым сиропом

• Все журналы \ Номер 10/181 `2002 от 11.03.2002 \ Математические пироги с кленовым сиропом

Константин НОСОВ

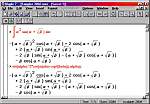
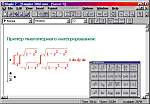
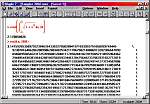
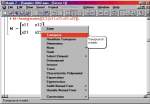
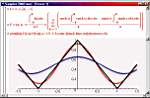
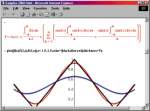
В одном из предыдущих номеров (МК № 3 (174)), в статье «Maple — кленовый символ математики», мы описали систему компьютерной математики Maple. Пришло время рассказать о применении этой программы для решения конкретных задач. Причем сконцентрируемся именно на тех из них, которые могут оказаться полезными, в первую очередь, школьникам и студентам.

Прежде всего познакомим читателей поближе с интерфейсом программы, поскольку о нем в предыдущем материале было сказано лишь вкратце. Итак, весь текст документа Maple делится на две части: активные строки ввода, передающие ядру системы свое содержимое для вычислений, и неактивные элементы, то есть результаты вычислений, заголовки секций, текстовые параграфы, неактивные математические формулы и графические объекты.

Типичная схема взаимодействия пользователя с системой выглядит так: в активную строку вводится выражение, которое по команде передается системе, после чего выводится результат вычислений (как правило, непосредственно за строкой ввода). Строка ввода вместе с результатом образуют ячейку, называемую Execution Group. На рисунке 1 показаны две такие ячейки: их можно распознать по объединяющей слева квадратной скобке. Maple позволяет также вычислять активные выражения в документе все сразу или примеры только из выделенной части.

В активную строку вводятся операторы, записанные в соответствии с синтаксисом системы. Для работы с программой, конечно, данный синтаксис придется изучить, к счастью для математиков это будет несложно. Так, основные математические функции имеют общепринятые обозначения, например, синус записывается как sin, а натуральный логарифм — как ln. Другие операторы тоже имеют близкое к естественному написание — тот же интеграл записывается как int. Кроме того, Maple предусматривает отображение математических выражений в традиционной математической символике. На том же рисунке 1, с точки зрения математики, активные выражения в первой и во второй квадратных скобках полностью идентичны, хотя записаны они по-разному.

Теперь перейдем непосредственно к решению математических задач. Традиционно начнем с основных операций анализа, к которым относятся предельный переход, нахождение производной и интеграла. Для проведения этих вычислений соответствующие операторы можно вводить с клавиатуры, но проще и быстрее воспользоваться специальной инструментальной панелью (рис. 2). В качестве примера подсчитаем объем шара единичного радиуса, для вычисления которого необходимо взять трехкратный интеграл. Если корректно расставить пределы интегрирования, Maple правильно определит объем :-), в чем можно убедиться, воспользовавшись известной со школьного курса формулой. Аналогичным образом предлагается находить площади фигур, объемы тел, поверхностные интегралы и т. п.

Если интеграл или какая-либо другая функция не могут быть записаны в символьном виде, Maple позволяет вести численный счет с наперед заданной точностью. Так, функция evalf подсчитывает значения выражений с количеством значащих цифр, задаваемых одним из ее аргументов. На рисунке 3 показаны примеры вычисления одного из интегралов эллиптического типа с 10-ью значащими цифрами и числа  (пи) с 1000-ью цифрами.

Теперь обратимся к задачам линейной алгебры. Без них не обходится ни один курс высшей математики вуза и даже школьная программа. Многим нашим читателям приходилось вычислять определители, обращать матрицы или решать системы линейных уравнений. Все, кто сталкивался с такими задачами, знают, каких усилий требует решение даже простейшей системы из трех уравнений, в которой коэффициенты не подобраны специальным образом.

Maple справляется с такими заданиями практически мгновенно. В системе существуют два специализированных пакета linalg и LinearAlgebra, содержащие функции для операций с матричными и векторными объектами. Кроме того, эти пакеты позволяют находить такие матричные характеристики, как собственные числа и собственные значения, базисы векторных пространств, различные разложения матриц, ранги и многое другое. Элементами матриц при этом могут быть не только числа, но и общие алгебраические выражениями, допустимые в системе.

Мы не будем останавливаться на конкретных задачах, а только покажем, насколько легко манипулировать с матричными объектами, не зная даже синтаксиса соответствующих операторов. Чтобы применить к матрице основные алгебраические функции, достаточно эту матрицу только ввести, после чего можно щелкнуть на ней правой кнопкой мыши и выбрать из контекстного всплывающего меню нужную функцию (рис. 4). Контекстное меню предлагает десяток-полтора наиболее важных применимых к данном объекту операторов. В нашем случае это операции транспонирования и эрмитового сопряжения, подсчета размерности, нормы (в четырех различных метриках), ранга матрицы, определителя и некоторые другие. Имеется также возможность вызова матричного редактора для покомпонентного просмотра и редактирования матрицы.

Перейдем теперь к графическим возможностям системы. Maple может строить большое количество графиков различных типов в двух и трех измерениях. Их вид варьируется в широких пределах. Специальными командами задаются вид осей координат, цвет и толщина кривых, шрифты для надписей и другие параметры. Для трехмерных графиков дополнительно предусмотрено задание типов отображения поверхности, шаг сетки, по которой вычисляются точки поверхности, координаты точки обзора и источника подсветки. Графики могут быть выведены в разных системах координат: как в привычной прямоугольной, так и в полярной, эллиптической, гиперболической, параболической и т. д. На одном графике можно отобразить произвольное число кривых или поверхностей.

Чтобы не обращаться к каким-нибудь искусственным примерам, для иллюстрации графических возможностей рассмотрим часто встречающуюся в курсах математики задачу приближение функции рядом Фурье. Попутно объясним, как в системе вводятся пользовательские функции, а также остановимся на некоторых других смежных вопросах.

Пользовательская функция (то есть не входящая в основной набор) задается с помощью двух ключевых операторов: присваивания ( обозначается «:=») и соответствия («->»). Например, чтобы задать линейную функцию f от переменной х, в строке ввода необходимо сделать такую запись:

f:=x->a*x+b

Она означает, что функция f ставит в соответствие числу х указанное выражение (a*x+b), что совпадает с классическим определением функции из школьного учебника. Задав таким образом функцию f, ее можно использовать во всех вычислениях наряду с внутренними функциями системы.

Вооружившись такими знаниями, нам несложно будет решить поставленную задачу. На рисунке 5 показаны все этапы этого процесса. В первой строке мы задаем приближаемую функцию. На интересующем нас участке (от –1.5 до 1.5) она представляет собой ломанную, но при повторении этого примера можно подставлять любую интересующую вас функцию. Во второй строке определена функция, задающая отрезок ряда Фурье. Эта функция зависит от двух аргументов: длины ряда n и координаты t. Maple позволяет, как видим, выписать ряд Фурье одним выражением. Не будем вдаваться в его синтаксис; главными операторами в этом выражении являются знакомые нам интегралы и оператор суммирования.

Наконец, с помощью функции plot выведем полученные результаты на график. А именно — выведем исходную функцию (отображена черным цветом) и ряды Фурье с двумя и четырьмя членами (соответственно синяя и красная кривые). Аргументами функции plot являются изображаемая функция или список функций, как в нашем случае, диапазон изменения абсцисс и дополнительные опции. Как видим, четырех членов ряда вполне хватает для достаточно точного приближения модельной функции. Если вы попробуете задать еще больше членов ряда Фурье, то он практически сольется с приближаемой функции.

Немногим сложнее получать графики в трехмерном пространстве. В этом случае используется функция plot3d, являющаяся естественным обобщением двумерной функции plot. В качестве аргументов здесь уже задаются функции, зависящие от двух переменных. Например, гиперболический параболоид можно визуализировать, введя такой оператор:

plot3d(x^2-y^2,x=-1..1,y=-1..1)

В результате получим график, показанный на рисунке 6.

Кроме статических графиков, система может создавать анимированные рисунки — как двух-, так и трехмерные. Для анимации, кроме обычных пространственных координат, соответствующих осям, вводится дополнительный аргумент, соответствующий времени. К сожалению, как выглядит анимация в Maple, проиллюстрировать на страницах журнала невозможно, но читатель без труда и сам разберется в этом вопросе.

Наконец, продемонстрируем взаимодействие Maple с интернет-форматами. Как указывалось в предыдущей статье, система имеет специальные средства для организации работы со спецификациями XML и MathML (каждый формат поддерживается особым пакетом). Однако обращение к этим исключительно мощным средствам требует глубокого изучения их синтаксиса, на что зачастую недостает времени. Намного чаще пользователю необходимо быстро опубликовать результаты своей работы в Сети для всеобщего доступа, даже за счет некоторой потери функциональности. Эта задача в системе решается в течение нескольких секунд и безо всяких усилий.

Maple позволяет экспортировать любой документ непосредственно в форматы MathML и HTML. Какой из них выбрать, зависит от того, на кого рассчитана ваша интернет-публикация. MathML специально предназначен для передачи математических текстов в Сети. Однако для просмотра в нем документов необходимо подключить к браузеру специальную надстройку (подробности смотрите в статье «Каков MathCAD в работе?», МК № 35 (154)), и нельзя быть на сто процентов уверенным, что все читатели вашей страницы выполнят это требование. Поэтому если вы хотите сделать документ доступным для всех, его лучше экспортировать в стандартный HTML-формат. Все математические символы и особенности оригинального документа при этом сохраняются (сравните рисунки 5 и 7, на которых соответственно отображены документ Maple и его экспортированная HTML-копия в Internet Explorer). При экспорте графические объекты преобразуются в GIF-файлы, причем точно передается не только цвет, форма и другие характеристики обычных графиков, но и все параметры движения анимированных рисунков. Кстати, Maple корректно экспортирует кириллицу, поэтому комментарии в своих документах можно смело писать на русском языке.

Понятно, что описанными примерами не исчерпывается весь потенциал возможностей системы Maple. В дальнейшем, возможно, к данной теме придется вернуться и описать новые актуальные задачи, решаемые с ее помощью. Однако надеемся, что и этот материал наглядно демонстрирует нашим читателям мощь и, что не менее важно, простоту этой программы при решении часто встречающихся учебных и практических задач.

Идёт загрузка...

Данную страницу никто не комментировал. Вы можете стать первым.

Ваше имя:
Ваша почта:
Комментарий:
Введите символы или вычислите пример: * Обновить